Method

液状化対策工法

グラベルドレーン工法（排水工法）の改良原理

グラベルドレーン工法（排水工法）は、高い透水性を有するドレーン材を地盤中に設置し、地盤の排水性を高めることで、地震時の過剰間隙水圧の上昇を抑え、液状化を防止する地盤改良工法です。
グラベルドレーン工法では透水性のよい砕石の柱を打設します。他にも人工排水材を打設するスパイラルドレーン工法などがあります。

排水工法の改良原理
排水工法の改良原理

グラベルドレーン工法（排水工法）の設計方法

グラベルドレーンの設計方法は「液状化対策工法設計・施工マニュアル (案) H11.3 建設省土木研究所他」の設計方法に従います。ドレーン配置算出手順は、下図に示すとおりです。

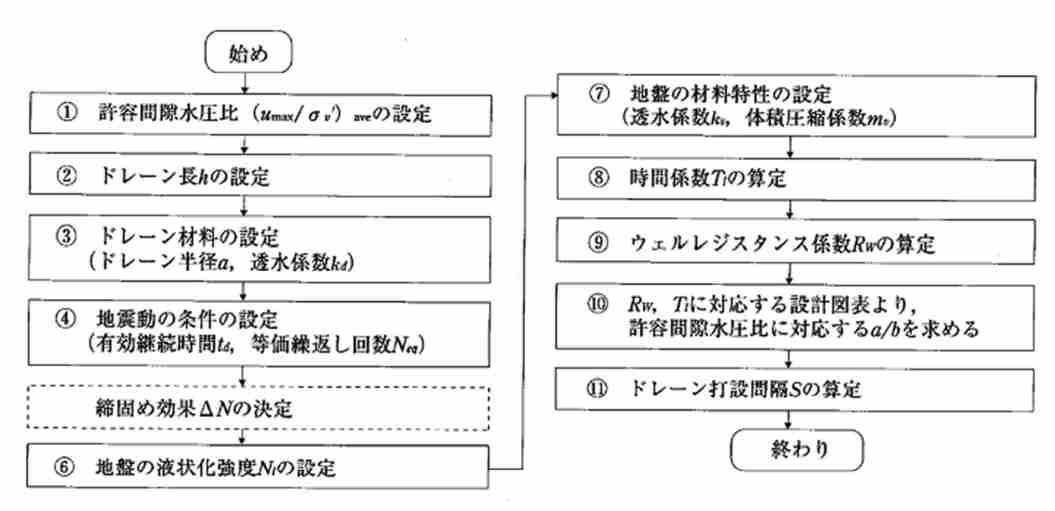
図-解4.9.5 ドレーンの配置算出の手順
図-解4.9.5 ドレーンの配置算出の手順

過剰間隙水圧消散の時間遅れ

ドレーンの打設間隔の設定では、「液状化対策工法設計・施工マニュアル（案）」に準じて、平均最大過剰間隙水圧と、a/b（a：ドレーンの半径、b：ドレーンの等価円柱の半径）の関係を表す設計図表を用います。その際に、ウェルレジスタンスによる過剰間隙水圧消散の時間遅れを次に示す方法により、地震動の有効継続時間tdを縮小補正することで考慮することができます。

ドレーンの透水係数は有限であるのでこの影響を考慮する必要がある。ここでは吉国らの解法を適用してドレーンの透水性を考慮する。すなわち、過剰間隙水圧消散の時間遅れTh(Rw)/Th(Rw=0)はウェルレジスタンス係数(Rw)と線形関係にあり、その傾きはb/aによって異なる。
過剰間隙水圧の時間遅れをBarron（バロン）の近似式を使って表せば、次式のようになる。

Th(Rw)
ここに、
F(n)＝

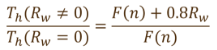
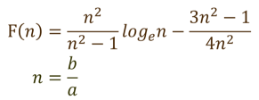
過剰間隙水圧の時間遅れは砂層の透水係数の低下、あるいは、消散に関する地震動有効継続時間の短縮と考えられるので、時間係数を縮小して基本方程式を解くことができる。

出典：液状化対策工法設計・施工マニュアル（案）, H11.3建設省土木研究所他, p.142～p.143

ドレーンの打設間隔の設定

以下にドレーンの打設間隔の標準的な設定方法を示す。

  1. 許容間隙水圧比の設定

    改良範囲の許容間隙水圧比は、円弧すべり計算を行って盛土が安定性を確保できるように設定するが、ドレーンによる間隙水圧抑制効果の特性からみて、0.5以下に設定する。既設盛土の法尻付近の対策においては、改良範囲を十分に広くできない場合がある。この場合には、許容間隙水圧比を小さく設定し、盛土の安定性を確保する必要がある。

  2. ドレーン長hの設定

    ドレーンは、完全液状化層の下端まで設置するのが標準的である。道路橋示方書では液状化の判定を行う必要がある土層を地下水面が現地盤面から10m以内にある沖積層で、かつ原地盤面から20m以内の範囲としているため、最大改良深度は原地盤面から20m以内となることが多いと考えられる。

  3. ドレーン材料の設定（ドレーン半径a、透水係数kd）

    グラベルドレーンが所要の透水係数を保持するためには、グラベルドレーンが目詰まりしないことが条件となる。 目詰まりしない概略の条件として、以下に示す提案がある。

    DG15/DG85＜9
    ここに、
    DG15
    ：排水材の15% 粒径（mm）
    DG85
    ：ドレーン周辺地盤の85%粒径（mm）

    砕石の透水係数の例を右に示す。

    図－解4.9.6 動水勾配に応じた砕石の透水係数14)
    図－解4.9.6 動水勾配に応じた砕石の透水係数14)
  4. 地震動の条件

    ドレーンの設計に用いる地震動の有効継続時間は、地震動そのものの継続時間ではなく、 Neqの継続時間である。 時松らは、過去の地震加速度波形を用いて、地震動の有効継続時間と地震マグニチュードの関係（図－解 4.9.9）を表し、その平均値として排水効果に関する地震動の有効継続時間を表－解 4.9.3のように表している。マグニチュードは、液状化判定で用いたマグニチュードと整合性をとる必要がある。

    表－解 4.9.3 排水効果に関する有効継続時間16)
    地震マグニチュードM 6 7 7.5 8
    有効継続時間td（s） 2 6 9 12
    a
    図－解 4.9.9 地震動の有効継続時間と地震マグニチュードの関係

    等価繰返し回数Neqは、複数の振幅τiを有する不規則波全体をτeなる単一応力レベルでの等振幅繰返しせん断波で置き換えるためのものである。Seed（シード）は、多くの加速度波形を検討した結果、地震マグニチュードMが大きいほどNeqが多くなる傾向を認め、τe=0.65τmaxとしたとき、表－解 4.9.4のようなMとNeqの関係を提案している。

    表解 4.9.4 τe=0.65 τmaxに対応する等価繰返し回数16)
    地震マグニチュード M 8.5 7.5 6.75 6 5.25
    有効継続時間td（s） 26 15 10 5 2～3
  5. 締固め効果

    ドレーン打設によりドレーン間の地盤のN値が増加するという事例が、 締固め式のグラベルドレーン、人工材ドレーンについて報告されている。 参考とし て一例を図－解 4.9.10に示す。これらのデータは、主に埋立て地盤での施工後の計測から得られたものである。 自然堆積地盤での適用性や土質特性および ドレーン仕様と地盤強度の増加との関係が明確でないため、 実際に適用する場合には試験施工などの実施により地盤強度の増加を確認することが望ましい。

    (a) グラベルドレーン (細粒分含有率 25~35%) (b) 人工材ドレーン
    図－解 4.9.10 ドレーン打設前後の原地盤N値の変化17）
  6. 地盤の液状化強度

    地盤の液状化強度を表す一定振幅で換算した地震動で液状化する繰返し回数(Nl)を適切に設定しなければならない。地盤の液状化強度の設定には、液状化判定で使用した情報が使用できる。Nlは室内試験結果から得られた液状化強度曲線より設定することができる。室内試験結果がない場合には、岩崎らによる次式により簡易的に算定することができる。

    NL=20×(1/FL)-1/0.17
    ここに、
    FL
    ：液状化抵抗率
  7. 原地盤透水係数

    透水係数は、現場透水試験を行った値がある場合はそれを使用し、試験が行われていない場合には、Creager（クレーガー）の方法などによって推定すればよい(表－解 4.9.5)。

    表解 4.9.5 Creager（クレーガー）によるD20と透水係数19）
    D20(mm) ks(cm/s) 土質分類 D20(mm) ks(cm/s) 土質分類
    0.005 3.00×10-6 粗粒粘土 0.18 6.85×10-3 微粒砂
    0.01 1.05×10-5 細粒シルト 0.20 8.90×10-3
    0.02 4.00×10-5 粗粒シルト 0.25 1.40×10-2
    0.03 8.50×10-5 0.30 2.20×10-2 中粒砂
    0.04 1.75×10-4 0.35 3.20×10-2
    0.05 2.80×10-4 0.40 4.50×10-2
    0.06 4.60×10-4 極微粒砂 0.45 5.80×10-2
    0.07 6.50×10-4 0.5 7.50×10-2
    0.08 9.00×10-4 0.6 1.10×10-1 粗粒砂
    0.09 1.40×10-3 0.7 1.60×10-1
    0.10 1.75×10-3 0.8 2.15×10-1
    0.12 2.60×10-3 微粒砂 0.9 2.80×10-1
    0.14 3.80×10-3 1.0 3.60×10-1
    0.16 5.10×10-3 2.0 1.80×10 細礫

    地盤の体積圧縮係数は、 繰返し三軸試験により求めた値を基本とするが、 試験結果がない場合には表－解 4.9.6 に示す値を用いてもよい。

    表解 4.9.6 砂の体積圧縮係数の値20）
    砂の種類 相対密度(%) 体積圧縮係数(cm2/kgf)
    シルト質砂 － 0.005～0.02
    緩い砂 20～40 0.005～0.01
    中位砂 40～60 0.002～0.005
    密な砂 60～80 0.001～0.002
    礫 － 0.0005～0.001
  8. 時間係数

    時間係数(Tl)は、式 (解 4.9.7) にしたがって計算する。

    Tl
    =ks・tl/(mv・yw・a2)
    ここに、
    ks
    ：地盤の透水係数（cm/s）
    tl
    ：Nl・td/Neq（s）
    Nl
    ：一定振幅に換算した地震動で液状化する繰返し回数
    td
    ：地震動の有効継続時間
    Neq
    ：地震動の等価繰返し回数
    mv
    ：地盤の体積圧縮係数（cm²/kgf）
    Yw
    ：水の単位体積重量(kgf/cm³)
    a
    ：ドレーンの半径（cm）

    時間係数はグラベルドレーンとプラスチックドレーンで異なり、グラベルドレーンは Tl=1～100 程度、プラスチックドレーンはTl=100～8000程度となる。

  9. ウェルレジスタンス係数

    ウェルレジスタンス係数(Rw)は,下式にしたがって計算する。

    Rw
    =(8/π²)・(ks/kd)・(h/a)³
    ここに、
    ks
    ：地盤の透水係数(cm/s)
    kd
    ：ドレーンの鉛直透水係数 (cm/s)
    h
    ：ドレーンの長さ(cm)
    a
    ：ドレーンの半径(cm)

    ウェルレジスタンス係数はグラベルドレーンとプラスチックドレーンで異なり、グラベルドレーンはRw=0.01～10程度、プラスチックドレーンはRw=0.1～10程度となる。

  10. 設計図表とドレーン等価有効円の半径

    各ドレーンの支配する砂層の等価円柱の半径（b）は、ウェルレジスタンス係数（Rw）および時間係数（T1）をパラメータとした設計図表より、許容間隙水圧比と対応させて求めた（a/b）から算定する。 設計図表は横軸がa/b、縦軸が平均最大過剰間隙水圧比となっている。設計図表の例を下に示す。

    図－6.5　平均間隙水圧比の最大値とドレーン間隔の関係
    図－6.5　平均間隙水圧比の最大値とドレーン間隔の関係

    出典：グラベルドレーン工法 技術資料, 平成8年4月1日, グラベルドレーン工法研究会, p.52

  11. ドレーンの打設間隔

    ドレーンの打設間隔（S）は、ドレーンの配置法にしたがって、下式により算定する。

    正方形配置
    ：S=1.77b
    正三角形配置
    ：S=1.90b
    ここに、
    b
    ：設計図表より求めたドレーンの等価有効円の半径

    配置法については、正方形配置でも正三角形配置でもかまわないが、通常は、施工機械の位置決めの容易さなどから正方形配置が採用されている。施工性の面からみて、ドレーンの最小打設間隔は、自然材料を用いた工法の場合1m程度、人工材料を用いた工法の場合0.5m程度である。

    出典：液状化対策工法設計・施工マニュアル（案）, H11.3建設省土木研究所他, p.141～p.152